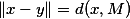内积 欧氏空间内积
线性空间
完备性
定义
设X是复线性空间,如果对于X中任意两个向量x,y,有一复数(x,y)与之对应,并且
满足如下条件:
1,
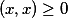 ,且
,且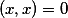 等价于
等价于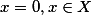
2,
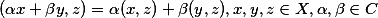
3,
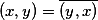
则称
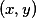 为x与y的内积,X称为内积空间.
为x与y的内积,X称为内积空间.令
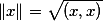
称为x的范数。
若X中范数完备,则称它为Hilbert(希尔伯特)空间
施瓦茨(Schwarz)不等式
设X按内积(x,y)成为内积空间,则对于X中的任意向量x,y,成立不等式:
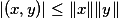
当且仅当x与y线性相关时,不等式等号才成立。
施瓦茨(Schwarz)不等式
投影定理
设X是度量空间,M是X的非空子集,x是X中的一点,称
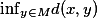
为点x到M的距离,记为 d(x,M),在赋范线性空间中
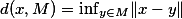 .
.定量 极小化向量定理
设X是内积空间,M是X中非空凸集,并且按X中由内积导出的距离完备,那么
对每个
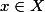 ,存在唯一的
,存在唯一的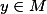 ,
,使得