数分：实数系基本定理

日期: 2010-07-27 分类: 数学/数学分析标签: publish
=== === === ===

确界存在定理实数连续性定理
非空有上界的数集必有上确界;非空有下界的数集必有下确界.

单调有界数列收敛定理
单调有界数列必定收敛.

定义
如果一列闭区间 $\{[a_n,b_n]\}$ 满足条件
(1) $[a_{n+1},b_{n+1}] \subset [a_n,b_n],n=1,2,\dots$
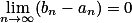
(2) $\lim_{n \to \infty } (b_n - a_n) =0$
则称这列闭区间形成一个闭区间套。

闭区间套定理
如果 $\{[a_n,b_n]\}$ 形成一个闭区间套,则存在唯一的实数 $\xi$
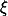
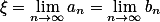属于所有的闭区间,且 $\xi=\lim_{n \to \infty}a_n =\lim_{n \to \infty}b_n$ .

Bolzano-Weierstrass 定理
有界数列必有收敛子列.

定义
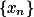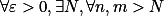如果数列 $\{x_n\}$ 具有以下特性： $\forall \varepsilon >0, \exists N,\forall n,m >N$ :
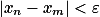
$|x_n-x_m| < \varepsilon$
则称数列 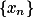$\{x_n\}$ 是一个基本数列.

Cauchy收敛原理
数列 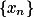$\{x_n\}$ 收敛的充分必要条件是: 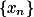$\{x_n\}$ 是基本数列.

Cauchy 收敛原理表明由实数构成的基本数列 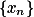$\{x_n\}$ 必存在实数极限，
这一性质称为实数系的完备性。

[注]通过数列来描述连续空间的性质.