练习:收敛准则应用
日期: 2010-07-27 分类: 数学/数学分析 标签: publish
=== === === ===
单调有界数列
定理 单调有界数列必定收敛
Fibonacci
数列
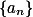 满足
满足
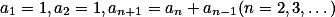 ,它的增长率
,它的增长率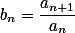
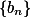 收敛于
收敛于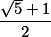 .
.
[Ex97]
Fibonacci数列的增长率
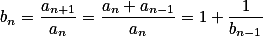
可以计算得出来:
如果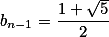 ,则
,则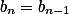 .
.
如果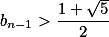 ,则
,则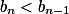 .
.
如果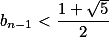 ,则
,则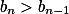 .
.
并且
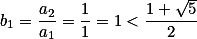 .
.
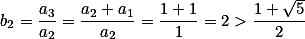
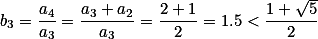
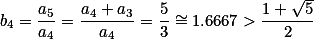
若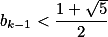
则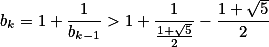 ,即
,即 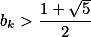 .
.
同样,可得若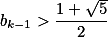 ,有
,有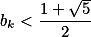 .
.
因此,综合上述计算有
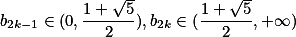 .
.
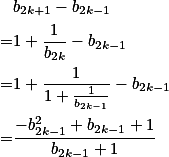
同样
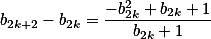
由于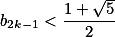 ,因此
,因此 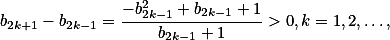
由于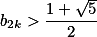 , 因此
, 因此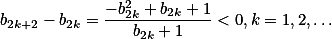
因此,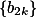 单调减少有下界
单调减少有下界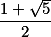 ,
,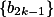 单调增加有上界
单调增加有上界 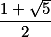
\pi
数列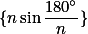 收敛于
收敛于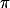
令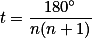 ,有
,有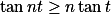
再有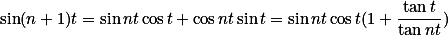 ,可得
,可得
出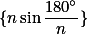 单调增加.
单调增加.
e
数列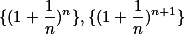 收敛于
收敛于
[Ex22]
数列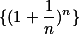 单调增加,
单调增加,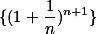 单调减少,两者收敛于同一极限。
单调减少,两者收敛于同一极限。
证 记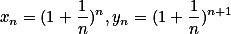 ,利用平均值不等式
,利用平均值不等式
![\sqrt[n]{ a_1 a_2 \dots a_n} \le \frac{a_1 +a_2 + \dots + a_n }{n} \quad (a_k \ge 0, k=1,2,\dots,n)](/data/mathimg/ex22_4.gif)
有
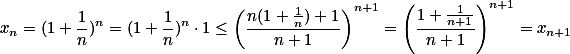
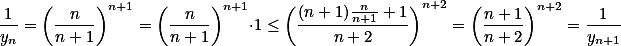
因此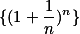 单调增加,
单调增加,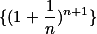 单调减少。
单调减少。
又
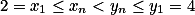 ,
,
因此,它们都 是有界数列,因而都收敛 。
并且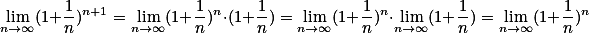
习惯上用字母e来表示这个极限。
记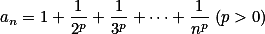
当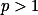 时,
时,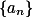 收敛,
收敛,
当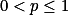 时
时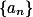 发散.
发散.
[Ex23]
Euler
常数
记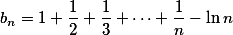 ,则数列
,则数列
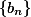 收敛,它的极限称为Euler常数.
收敛,它的极限称为Euler常数.
证 首先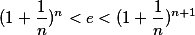 ,
,
同时取对数
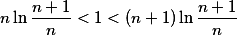
因此
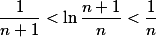
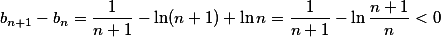
因此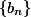 单调减少。
单调减少。
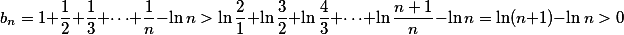 ,
,
这说明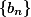 是单调有下界的数列,因而收敛 。
是单调有下界的数列,因而收敛 。
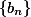 的极限
的极限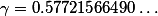 称为Euler常数.
称为Euler常数.
[Ex24]
求极限 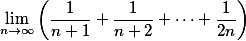
解,在Ex23中,我们已经证明
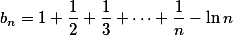 ,数列
,数列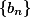 收敛
收敛
令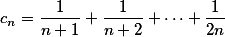 ,则
,则
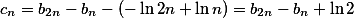
由于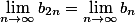 ,
,
因此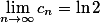
[Ex25]
求极限 ![\lim_{n \to \infty } [1 - \frac{1}{2} + \frac{1}{3} - \dotsb + (-1)^{n+1} \frac{1}{n}]](/data/mathimg/ex25_1.gif)
解令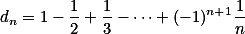 .
.
由Ex23
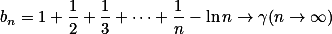
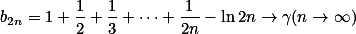
考虑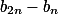 ,用
,用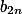 的第2k项减去
的第2k项减去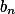 第k项,
第k项,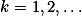 ,有
,有
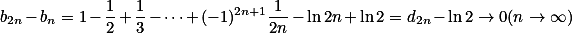
因此
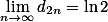
又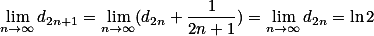
因此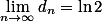
Cauchy
收敛准则
[Ex27]
设数列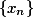 满足压缩性条件:
满足压缩性条件:
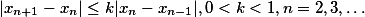 ,则
,则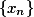 收敛.
收敛.
证明,首先,对于所有n>0,
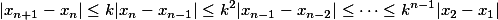
对于任意的m>n,
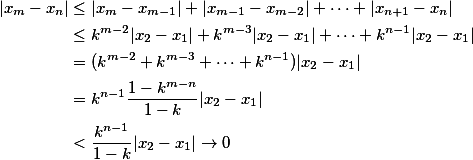
因此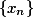 基本数列,由Cauchy收敛原理(Cauchy收敛原理),
基本数列,由Cauchy收敛原理(Cauchy收敛原理),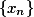 收敛。
收敛。
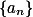 满足
满足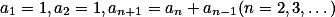 ,它的增长率
,它的增长率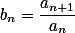
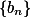 收敛于
收敛于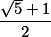 .
.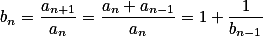
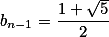 ,则
,则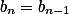 .
.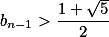 ,则
,则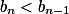 .
.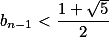 ,则
,则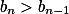 .
.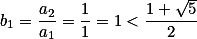 .
.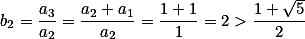
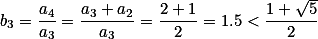
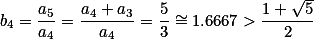
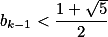
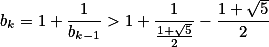 ,即
,即 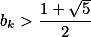 .
.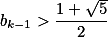 ,有
,有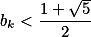 .
.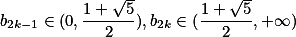 .
.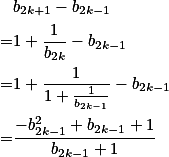
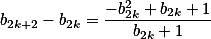
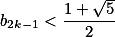 ,因此
,因此 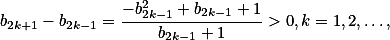
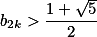 , 因此
, 因此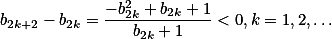
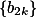 单调减少有下界
单调减少有下界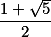 ,
,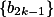 单调增加有上界
单调增加有上界 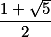
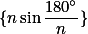 收敛于
收敛于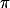
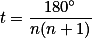 ,有
,有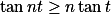
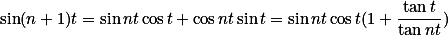 ,可得
,可得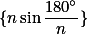 单调增加.
单调增加.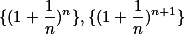 收敛于
收敛于
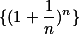 单调增加,
单调增加,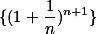 单调减少,两者收敛于同一极限。
单调减少,两者收敛于同一极限。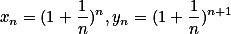 ,利用平均值不等式
,利用平均值不等式![\sqrt[n]{ a_1 a_2 \dots a_n} \le \frac{a_1 +a_2 + \dots + a_n }{n} \quad (a_k \ge 0, k=1,2,\dots,n)](/data/mathimg/ex22_4.gif)
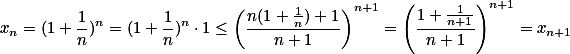
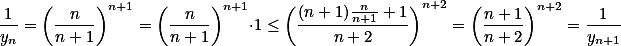
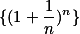 单调增加,
单调增加,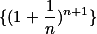 单调减少。
单调减少。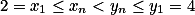 ,
,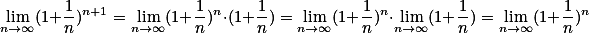
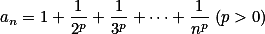
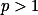 时,
时,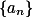 收敛,
收敛,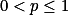 时
时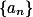 发散.
发散.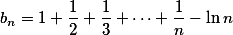 ,则数列
,则数列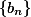 收敛,它的极限称为Euler常数.
收敛,它的极限称为Euler常数.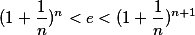 ,
,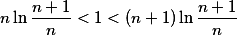
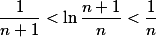
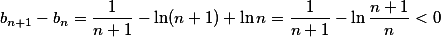
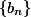 单调减少。
单调减少。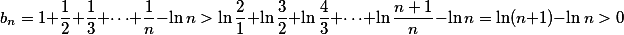 ,
,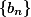 是单调有下界的数列,因而收敛 。
是单调有下界的数列,因而收敛 。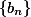 的极限
的极限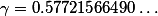 称为Euler常数.
称为Euler常数.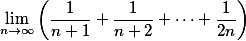
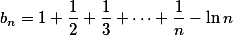 ,数列
,数列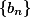 收敛
收敛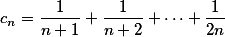 ,则
,则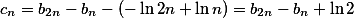
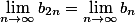 ,
,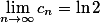
![\lim_{n \to \infty } [1 - \frac{1}{2} + \frac{1}{3} - \dotsb + (-1)^{n+1} \frac{1}{n}]](/data/mathimg/ex25_1.gif)
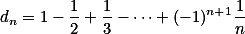 .
.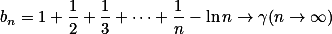
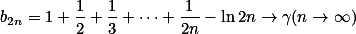
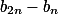 ,用
,用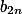 的第2k项减去
的第2k项减去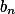 第k项,
第k项,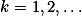 ,有
,有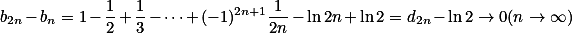
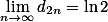
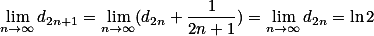
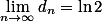
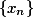 满足压缩性条件:
满足压缩性条件: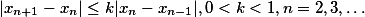 ,则
,则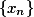 收敛.
收敛.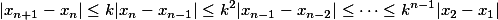
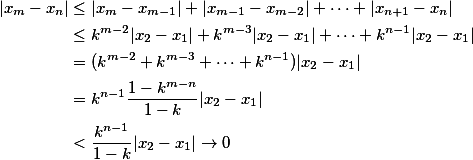
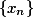 基本数列,由Cauchy收敛原理(Cauchy收敛原理),
基本数列,由Cauchy收敛原理(Cauchy收敛原理),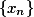 收敛。
收敛。