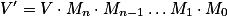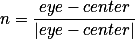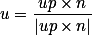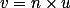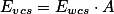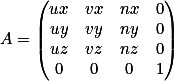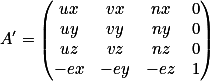仿真:osg的matrix与坐标变换
日期: 2022-06-07 标签: publish
=== === === ===
平面绘制时,线条的绘制的实现统一是在XOY平面进行绘制。
如果要在任意一面进行绘制,如果它的坐标轴向量为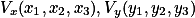 ,需要映射到
,需要映射到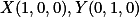 .
.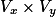 映射到Z.
映射到Z.
顶点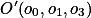 映射到点
映射到点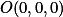 . 在绘制的时候得到的是XOY坐标系的坐标,需要求它在平面坐标系的坐标。
. 在绘制的时候得到的是XOY坐标系的坐标,需要求它在平面坐标系的坐标。
[Ex129]
线性代数关于坐标变换
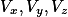 的坐标分别为
的坐标分别为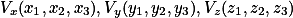
这样平面的坐系到X,Y,Z的过渡矩阵为
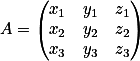
同一向量在XYZ坐标系的坐标为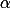 ,那么在平面坐标系的坐标为
,那么在平面坐标系的坐标为
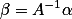
这里
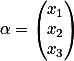
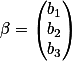
这是因为
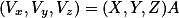
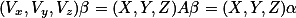
因此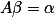
再考虑坐标平移,同一点P,有
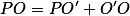
设在平移后坐标系下的坐标为
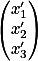
有
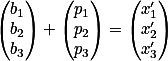
[Ex130]
osg
的矩阵
osg::Matrix mat1; //定义-一个单位矩阵
mat1.makeRotate( osg::Quat(osg::PI_2, osg::Vec3(1.0, 0.0, 0.0)); //旋转
mat1.preMultTranslate( osg::Vec3d(0.0, 1.0, 0.0) ); //再执行Y方向的平移
osg::Vec3d vec(0.0, 0.0, 1.0);
vec= vec * mat3; //将矩阵用于向量的空间变换
此处最终对向量vec进行了空间变换。变换矩阵可以视为几个动作的效果叠加:先执行Z方向的
放大,再执行X方向的旋转,最后执行Y方向的平移。注意,此处使用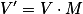 的形式来表达向量
的形式来表达向量
的空间变换计算,即矩阵M左乘一个行向量V,这是OSG中唯-正确的向量变换表达方式。
但是OSG也支持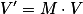 的形式,即矩阵M右乘一个列向量V.这事实上可以理解为这样的形式:
的形式,即矩阵M右乘一个列向量V.这事实上可以理解为这样的形式:
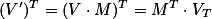
即向量V与M的转置(Transpose)矩阵的相乘。由于OSG中不对行向量与列向量进行区分,因
此有时这样的做法可以迅速得到所需的结果,而不必再手动对矩阵进行转置操作。
osg
的空间变换
在相对参考系中定义的一个顶点位置的局部坐标,往往并非这个顶点在世界中的真实坐标,为了
实现局部坐标和世界坐标的换算,就需要将各级相对坐标系的变换矩阵进行级联,即通过各级变换矩
阵的相乘,合并多个矩阵变换的效果,并进而得到坐标在合并后的变换矩阵作用下的计算结果。
OSG中使用行主序(row -major)矩阵实现变换操作,而表达一个空间矢量
则使用行向量。因此,表达一个向量V经过矩阵M变换得到的计算结果V'的公式如下:
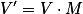
如果试图将某级局部坐标系 下的顶点V变换为世界坐标V' ,则需要将各级局部坐标系的变换矩
阵依次相乘。假设在世界坐标系下变换矩阵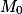 ,依次累积,直至V所在局部坐标系的变换矩阵
,依次累积,直至V所在局部坐标系的变换矩阵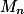 ,
,
那么级联矩阵得到V'的公式如下。
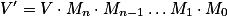
相机节点模型视点矩阵
在VCS坐标系下,习惯使用n、u、v3个分量来表示坐标基向量(Coordinate Basis Vector)。分
量n是一个从参考点center指向视点eye的向量,相当于世界坐标系的Z轴;分量u是视点上方向up
与n的叉积,相当于X轴;而v分量是n与u的叉积,相当于Y轴。使用数学公式进行表达:
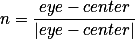
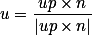
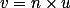
WCS坐标系下的坐标基向量为X (1,0,0) 、Y (0,1,0)、z (0,0,1),由此得到wCS
向VCS的过渡矩阵A.
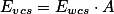
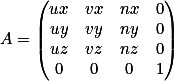
注意上面的变换公式没有考虑相机坐标系原点和世界坐标系原点的偏移关系,将这一偏置过程考
虑在公式中,则有:
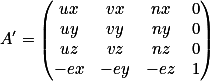
它事实.上也就是模型视点矩阵的内容。
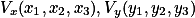 ,需要映射到
,需要映射到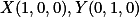 .
.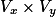 映射到Z.
映射到Z.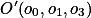 映射到点
映射到点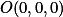 . 在绘制的时候得到的是XOY坐标系的坐标,需要求它在平面坐标系的坐标。
. 在绘制的时候得到的是XOY坐标系的坐标,需要求它在平面坐标系的坐标。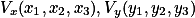 ,需要映射到
,需要映射到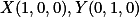 .
.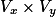 映射到Z.
映射到Z.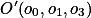 映射到点
映射到点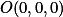 . 在绘制的时候得到的是XOY坐标系的坐标,需要求它在平面坐标系的坐标。
. 在绘制的时候得到的是XOY坐标系的坐标,需要求它在平面坐标系的坐标。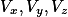 的坐标分别为
的坐标分别为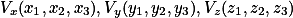
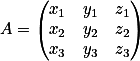
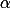 ,那么在平面坐标系的坐标为
,那么在平面坐标系的坐标为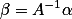
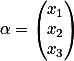
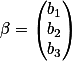
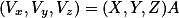
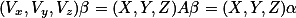
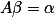
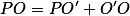
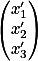
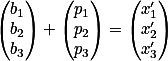
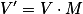 的形式来表达向量
的形式来表达向量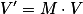 的形式,即矩阵M右乘一个列向量V.这事实上可以理解为这样的形式:
的形式,即矩阵M右乘一个列向量V.这事实上可以理解为这样的形式: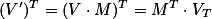
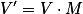
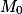 ,依次累积,直至V所在局部坐标系的变换矩阵
,依次累积,直至V所在局部坐标系的变换矩阵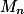 ,
,