设
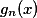是定义在[a,b]上的可积函数,(n=0,1,2,...),若对任意的m和n,
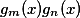在[a,b]上可积，且有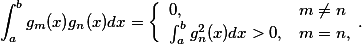
则称
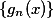是[a,b]上的正交函数列。特别地，当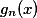
是n次多项式时，称
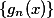是[a,b]上的正交多项式n次Legendre多项式
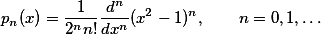
是[-1,1]上的正交多项式.
[Ex389]
正交函数有什么作用？
role1:
### 正交函数的作用
正交函数的核心思想是“正交性”，类似于向量空间中的垂直向量，这使得它们在许多领域非常有用。以下是正交函数的主要作用：
1. **函数展开和近似**：
- 正交函数常用于将复杂函数展开为级数形式，类似于傅里叶级数。例如，在信号处理中，正交基函数（如正弦和余弦）用于表示信号，从而进行压缩、滤波或分析。
- 在数值分析中，正交多项式（如Legendre、Chebyshev多项式）用于多项式近似和最小二乘拟合，可以更高效地逼近函数，减少误差。
2. **求解微分方程**：
- 许多物理问题涉及的微分方程（如拉普拉斯方程、波动方程）的解可以用正交函数表示。例如，在量子力学中，波函数常用Hermite多项式（用于谐振子）或Legendre多项式（用于球对称问题）展开。
- 在工程中，正交函数用于分离变量法，简化偏微分方程的求解。
3. **数值积分和求积方法**：
- 正交多项式的零点用于高斯求积法（Gaussian quadrature），这是一种高效的数值积分技术。例如，Legendre多项式的零点用于计算定积分，精度较高。
4. **内积空间和泛函分析**：
- 在数学中，正交函数构成完备正交系，用于构建Hilbert空间的基。这允许函数被唯一表示为线性组合，便于分析函数的性质和收敛性。
5. **物理学和工程应用**：
- 在电磁学中，正交函数用于求解麦克斯韦方程，特别是在波导和天线设计中。
- 在热传导和流体力学中，正交函数用于表示温度分布或流速场。
- 在振动分析中，正交模式用于描述结构的自然频率和模态。
6. **信号处理和图像处理**：
- 正交变换（如傅里叶变换、小波变换）基于正交函数，用于频域分析、数据压缩（如JPEG）和噪声去除。
### 以Legendre多项式为例
从笔记中，Legendre多项式在
上正交，它们特别用于：- **球坐标系问题**：在物理学中，如 gravitational potential 或电磁场 in spherical coordinates，Legendre多项式出现在球谐函数中。
- **数值方法**：在高斯求积中，Legendre多项式的零点作为积分点，提高计算效率。
role2
作为role2，我认为role1的分析已经很全面，但我可以从几个角度补充一些内容：
### 1. 正交性与线性代数的类比理解
正交函数的概念实际上是线性代数中向量正交的推广。在有限维空间中，如果两个向量的点积为零，则称它们正交。同样，在函数空间中，如果两个函数的"内积"（即积分∫g_m(x)g_n(x)dx）为零，则称这两个函数正交。这种类比有助于我们理解为什么正交函数系可以作为函数空间的"基"。
### 2. Legendre多项式的具体应用
除了role1提到的应用外，Legendre多项式还在以下领域有重要应用：
- **量子力学**：在氢原子问题的求解中，角度部分会用到Legendre多项式
- **计算机图形学**：在球面光照计算和环境映射中，Legendre多项式用于球谐函数的表示
- **地球物理学**：用于表示地球引力场和磁场模型
### 3. 数据分析和机器学习中的应用
正交函数在现代数据分析中也扮演着重要角色：
- **特征提取**：正交基可以用于提取数据的互不相关的特征
- **降维技术**：如主成分分析(PCA)本质上是在寻找数据的最优正交基
- **正交多项式回归**：使用正交多项式进行回归分析可以避免多重共线性问题
### 4. 计算优势
使用正交函数系有许多计算上的优势：
- **数值稳定性**：由于正交性，系数计算更加稳定，减少了舍入误差的累积
- **简化计算**：在展开函数时，各系数可以独立计算，无需解方程组
- **收敛性**：正交级数通常具有更好的收敛性质
### 5. 其他重要的正交多项式族
除了Legendre多项式外，还有其他重要的正交多项式系：
- **Chebyshev多项式**：在[-1,1]上关于权重1/√(1-x²)正交，广泛用于逼近论
- **Hermite多项式**：在(-∞,∞)上关于权重e^(-x²)正交，用于量子力学和谐振子问题
- **Laguerre多项式**：在[0,∞)上关于权重e^(-x)正交，用于氢原子模型的径向部分
这些不同的正交多项式系各自适用于不同的区间和权重函数，使得它们在特定问题中特别有用。
总而言之，正交函数不仅是数学理论中的重要概念，也是解决实际问题的强大工具。