设f(x)是定义在可测集
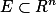 的实函数,如果
的实函数,如果对于任意有限实数a,
![E[f >a]](/data/mathimg/m509_2.gif) 都是可测集,则称f(x)定义在E
都是可测集,则称f(x)定义在E上的可测函数.
定理
设f(x)是定义在可测集E上的实函数,下列任一条件都是f(x)在E上可测的充要条件:
1,对任何有限实数a,
![E[f \ge a]](/data/mathimg/m509_3.gif) 都可测
都可测2,对任何有限实数a,
![E [f <a]](/data/mathimg/m509_4.gif) 都可测。
都可测。3,对任何有限实数a,
![E[f \le a ]](/data/mathimg/m509_5.gif) 都可测。
都可测。定理
可测集
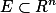 上的连续函数都是可测函数。
上的连续函数都是可测函数。定理
(1) 设f(x)是可测集E上可测函数,而
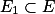 为E的可测子集,
为E的可测子集,则f(x)是看作定义在
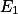 上的函数时,它是
上的函数时,它是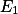 上
上的可测函数
(2) 设f(x)是定义在有限个可测集
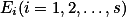 的并集
的并集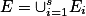 上,且f(x)在每个
上,且f(x)在每个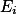 上可测,则f(x) 在E上也可测。
上可测,则f(x) 在E上也可测。引理
设 f(x) 与 g(x)为有上可测函数,则
![E[f >g]](/data/mathimg/m509_13.gif) 与
与![E[f \ge t]](/data/mathimg/m509_14.gif) 都是可测集。
都是可测集。设f(x),g(x)在E上可测,则下列函数(假定它们在E上有意义)皆在E上可测:
(1) f(x)+g(x)
(2) |f(x)|
(3)
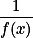
(4)
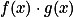
定义3:设
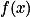 的定义域
的定义域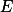 可分为有限个互不相交的可测集
可分为有限个互不相交的可测集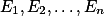 ,且
,且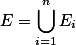 ,使得
,使得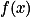 在每个
在每个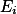 上都等于某常数
上都等于某常数 ,则称
,则称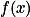 为简单函数。
为简单函数。定理5:设
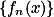 是
是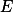 上一列(或有限个)可测函数,则
上一列(或有限个)可测函数,则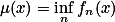 与
与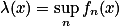 都在
都在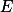 上可测。
上可测。定理6:设
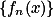 是
是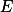 上一列可测函数,则
上一列可测函数,则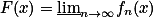 ,
,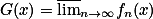 也在
也在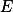 上可测,特别当
上可测,特别当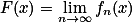 存在时,它也在
存在时,它也在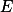 上可测。
上可测。定理7(可测函数与简单函数的关系):设
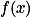 在
在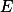 上可测,则
上可测,则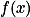 总可以表示成一列简单函数
总可以表示成一列简单函数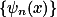 的极限函数
的极限函数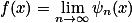 ,而且还可办到
,而且还可办到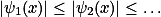 。
。定义 4 设π是一个与集合
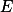 的点
的点  有关的命题;如果存在子集
有关的命题;如果存在子集 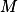 ,适合
,适合 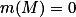 ,使得π在
,使得π在 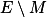 上恒成立,也就是,
上恒成立,也就是,![E \setminus E[\pi \text{ holds true}]](/data/mathimg/m509_48.gif) 是零测度集,则我们称π在
是零测度集,则我们称π在 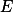 上几乎处处成立,或说 a.e. 于
上几乎处处成立,或说 a.e. 于 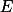 成立。
成立。引理 设
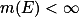 ,
,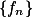 是
是 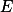 上的一列几乎处处有限的可测函数;若
上的一列几乎处处有限的可测函数;若 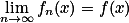 a.e. 于
a.e. 于 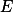 ,且
,且 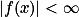 a.e. 于
a.e. 于 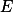 ,则对任意
,则对任意 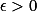 和任意正整数
和任意正整数 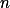 ,作
,作 ![E[n,\epsilon] = E[|f_k - f_{n}| < \epsilon, k \geq n]](/data/mathimg/m509_60.gif) ,我们有
,我们有 ![\lim_{n \rightarrow \infty} m(E \setminus E[n,\epsilon]) = 0](/data/mathimg/m509_61.gif) 。
。推论 设
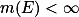 ,
,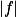 是
是 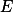 上的一列 a.e. 收敛于一个 a.e. 有限的函数
上的一列 a.e. 收敛于一个 a.e. 有限的函数 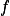 的可测函数列,则对任意
的可测函数列,则对任意 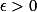 有
有 ![\lim m(E \setminus E[|f_{n} - f| < \epsilon]) = 0](/data/mathimg/m509_67.gif) 。
。定理 (EropoB) 设
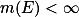 ,
,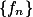 是
是 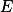 上的一列 a.e. 收于一个 a.e. 有限的函数
上的一列 a.e. 收于一个 a.e. 有限的函数 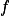 的可测函数,则对任意
的可测函数,则对任意 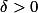 ,存在子集
,存在子集 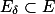 ,使
,使 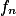 在
在 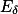 上一致收敛,且
上一致收敛,且 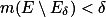 。
。