外测度
可测定义 (卡拉泰奥多里)
设E为
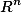 中的点集,如果对于任一点集T 都有
中的点集,如果对于任一点集T 都有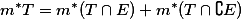
则称E是L可测的,这时E的L外测度
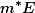 即称为E的L测度,
即称为E的L测度,记为
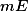
L可测集全体记为
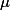 .
.定理
集合E可测的充要条件是对于任意的
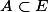 ,
,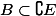 ,总用
,总用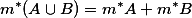
定理
S可测的充要条件是
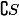 可测。
可测。定理
设
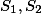 可测,则
可测,则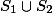 也可测,
也可测,并且当
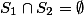 时,对于任意集合T总有
时,对于任意集合T总有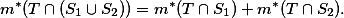
定理
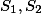 都可测,则
都可测,则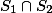 也可测。
也可测。定理
设
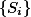 是一列互不相交的可测集,则
是一列互不相交的可测集,则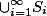 也是可测集,且
也是可测集,且 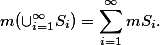
推论
设
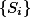 是一列可测集,则
是一列可测集,则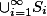 也是可测集。
也是可测集。定理
设
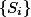 是一列可测集,则
是一列可测集,则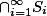 也是可测集。
也是可测集。设
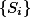 是一列递增的可测集:
是一列递增的可测集: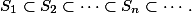
令
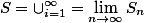 ,则
,则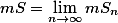
定理
设
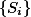 是一列递降的可测集合:
是一列递降的可测集合: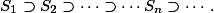
令
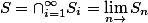 ,则
,则当
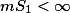 时,
时,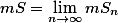 .
.