见<常微分方程>P158
n阶贝赛尔(Bessel)方程:
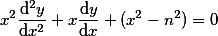
一般的,考虑二阶齐线性方程
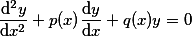
如果方程的系数
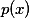 和
和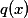 都能展成x的幂级数,且收敛
都能展成x的幂级数,且收敛区间为
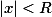 ,则方程有形如
,则方程有形如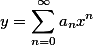
的特解,也以
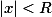 为级数的收敛区间.
为级数的收敛区间.若方程中系数
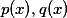 具有这样的性质,即
具有这样的性质,即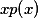 和
和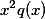 均能展成x的幂级数,且收敛区间为|x| <R,则方程有形如
均能展成x的幂级数,且收敛区间为|x| <R,则方程有形如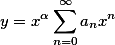
的特解,这里
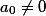 ,
,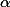 是一个特定的常数.级数
是一个特定的常数.级数也以
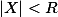 为收敛区间.
为收敛区间.可解得贝赛尔方程的一个特解
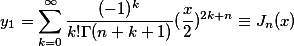
称为n阶贝赛尔函数.
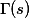 定义如下:
定义如下:当
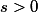 时,
时,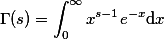 ;当
;当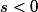 且非整数时,由递推公式
且非整数时,由递推公式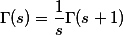 定义.它具有性质:
定义.它具有性质: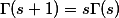 ;
;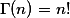 ,n为正整数.
,n为正整数.
见<常微分方程>P158
n阶贝赛尔(Bessel)方程:
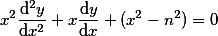
一般的,考虑二阶齐线性方程
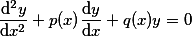
如果方程的系数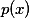 和
和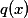 都能展成x的幂级数,且收敛
都能展成x的幂级数,且收敛
区间为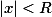 ,则方程有形如
,则方程有形如
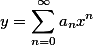
的特解,也以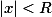 为级数的收敛区间.
为级数的收敛区间.
若方程中系数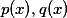 具有这样的性质,即
具有这样的性质,即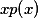 和
和
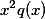 均能展成x的幂级数,且收敛区间为|x| <R,则方程有形如
均能展成x的幂级数,且收敛区间为|x| <R,则方程有形如
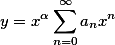
的特解,这里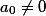 ,
,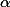 是一个特定的常数.级数
是一个特定的常数.级数
也以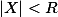 为收敛区间.
为收敛区间.
可解得贝赛尔方程的一个特解
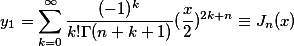
称为n阶贝赛尔函数.
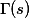 定义如下:
定义如下:
当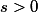 时,
时,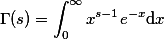 ;当
;当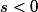 且非整数时,由递推公式
且非整数时,由递推公式
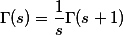 定义.它具有性质:
定义.它具有性质:
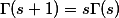 ;
;
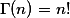 ,n为正整数.
,n为正整数.