P208
拉格朗日在＜关于代数方程的思考＞一文试图证明五次及更高的方程不可能像二、三、四
次方程那西游记求解，但经过顽强的努力之后不得不坦言这个问题“好像是在向人类的智
慧提出挑战”，迎接着一挑战的是挪威的年仅22岁的阿贝尔，他于1824年在自费出版的一本
小册了＜论代数方程，证明一般五次方程的不可解性＞，在其中严格证明了以下事实：如
果方程的次数
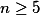,并且系数
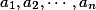看成字母，那么任何一个由这些字母组成的根式都不可能是方程的根。他还考虑了一些特殊的
能用根式求解的方程，其中一类被现在称为“阿贝尔方程”，这一工作中，他实际引进了域
这一重要的近世代数数的概念。
阿贝尔只活了27岁，他一生贫病交加，但却留下了许多创造性的贡献。他毕业后长期找不到
工作。
阿贝尔只是证明了对于一般的五次或五次以上的方程根式解是不可能的，但不妨碍人们去求
一些特殊的代数方程。
在阿贝尔工作之后，数学家所面临的一个问题是：什么样的特殊方程能够用根式？法国
青年数学家伽罗瓦(G.Galois)在1892－－1831年间完成的几篇论文中建立了判别方程根式
可解的充分必要条件。从而宣告了方程根式可解这一经历三百年的难题的彻底解决。
伽罗瓦的思想是研究n次方程的n个根的排列的置换，提出了群的概念。不过它所指的群只是
具体的置换群。他考虑了它的一个子群“方程的群”现称之“伽罗瓦群”，属于该子群的置换使得方程的根以由方程系数
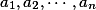生成的域为系数的全部代数关系不变。伽罗瓦证明当且仅当方程的群满足一定的条件进方程才是根式可解的。
拉格朗日已经讨论过方程根的置换并意识到置换理论是“整个问题的真正的哲学”。
伽罗瓦生逢法国大革命的动荡时代。他的思想大超出了他的时代。他的工作可以看作是近似代
数的发端。这不只是因为它解决了方程根可解这样一个难题，更重要的是群的概念的引进导
致了代数学在对象、内容和方法上的深刻变革。
19世纪后半叶，数学家们双认识到，“群”可以是一个更加普遍的概念，而不必仅限于置换
群。凯莱(A.Cayley)在1849--1854年间指出矩阵在乘法下、四元数在加法下都构成群，人们
发现高斯在数论中研究过的具有同一判别式的二次型类
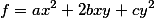
对于型的合成运算也构成群.1868--1869年若当尔(C.Jordan)在物理学家布拉维斯(A.Bravais)
关于运动群的理论的启发下开展了无限群的系统研究。若尔当的工作又影响了克莱因
(F.Klein)关于几何分类中的无限变换群的研究，1874－－1853年间，挪威数学家李(S.Lie)又
研究了无限连续变换群（李群),到19世纪80年代，关于各种不同类型的群的研究使数学家们
有了足够的积累来形成抽象群的概念。在抽象群的概念中，集合元素本身的具体内容无关
紧要，关键是联系这些元素的运算关系。这样建立起来的一般群论是描写其他各种数学与
物理现象的对称性质的普遍工具。
代数学由于群的概念的引进和发展而获得新生。它不再仅仅是研究代数方程，而更多地是研
究各种抽象的“对象”的运算关系，19世纪中叶以后，这种抽象的“对象”层出不穷，从而
为20世纪代数结构观念的产生奠定了基础。