P193
在18世纪出现的数学分支中,变分法的诞生最富有戏剧性,变分法起源于“最速降线”和其他
一些类似问题。所谓最速降线问题,是要求给出两点之间一条曲线,使质点在重力作用下沿
着它由一点至另一点降落最快。这问题最早由约翰.伯努利提出来向其他数学家挑战。
牛顿和雅布.伯努利等人的研究意不仅在于给出了正确的答案,更重要的是揭示了这一问题区别
于普通极值问题的特征。因些这些工作与同时期出出的等周问题(求具有给定弧长的曲线,使
其面积最大,属带附加条件的问题),测地线问题(求曲面上两点之间的最短路径)等标志着一
门新数学分支--变分法的诞生。
变分法处理的是一个全新的课题:求变量
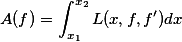
的极大值或极小值,A(f)是函数的函数。
欧拉和拉格朗日分别给出了f是极值的必要条件,欧拉的变分法在许多地方还依赖于几何论证,
而拉格朗日则在纯分析的基础上建立了变分法。拉格朗日第一次成功地处理了端点变动的极
值曲线问题及重积分情形,1770年后又研究了被积函数中含有高阶导数的变分问题,这些问
题后来都成为变分法的标准内容。