证明见零点存在定理证明
有界性定理
若函数f(x)在闭区间[a,b]上连续,则它在[a,b]上有界.
最值定理
若函数f(x)在闭区间[a,b]上连续,则它在[a,b]上必能取到
最大(小)值,即存在
![\xi,\eta \in [a,b]](/data/mathimg/m22_1.gif) ,对于一切
,对于一切![x \in [a,b]](/data/mathimg/m22_2.gif) 成立
成立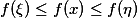 .
.零点存在定理
若函数f(x)在闭区间[a,b]连续,且
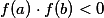 ,则存在
,则存在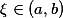 ,使
,使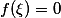
中间值定理
若函数f(x)在闭区间[a,b]上连续,则它一定能取到最大值
![M=\max \left\{f(x) \middle| x \in [a,b] \right \}](/data/mathimg/m22_7.gif) 和
和最小值
![m=\min \left\{f(x) \middle| x \in [a,b] \right\}](/data/mathimg/m22_8.gif) 之间的任何一个值.
之间的任何一个值.Cantor定理
若函数f(x)在闭区间[a,b]上连续,则它在[a,b]上一致连续.
一致连续
设函数在区间X上定义,若对于任意给定的
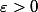 ,存在
,存在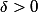 ,
,只要
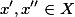 满足
满足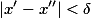 ,就成立
,就成立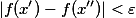 ,则称函数f(x)在区间X上一致连续.
,则称函数f(x)在区间X上一致连续.定理 设函数f(x)在区间X上定义,则f(x)在X上一致连续的充分必要条件是:对于任何点列
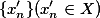 和
和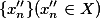 ,
,只要满足
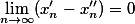 ,就成立
,就成立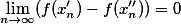 .
.定理 函数f(x)在有限开区间(a,b)上连续,则f(x)在(a,b)上一致连续的充要条件是:f(a+)和f(b-)存在。
============
看多元函数的情形
连续映射将紧集映射成紧集。
它可以推出
1.有界性定理 设f(x)是紧集
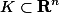 上的连续函数,则f(x)
上的连续函数,则f(x)在K上有界.
2. 最值定理 设f(x)是紧集
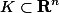 上的连续函数,则它在
上的连续函数,则它在K上必能取到最大值和最小值,即存在
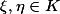 ,对于一切
,对于一切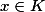 成立
成立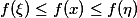 .
.一致连续定理 设K是
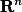 中点集,
中点集,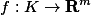
为连续映射,那么f(x)在K上一致连续.
连续映射将连通集映射成连通集。